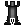Lembro-me da primeira vez em que joguei Carcassonne, e uma amiga me disse, no final da partida: "Que jogo interessante! O tabuleiro é diferente a cada partida e fica bem bonito". De fato, este é, para mim e para muita gente, o grande apelo dos jogos de colocação de peças (ou tile placement) e os de tabuleiro modular em geral: variedade entre as partidas e um sensação de beleza ao se construir o cenário do jogo por meio das diferentes peças disponíveis.
Acredito que tal apelo já existia antes de Carcassonne e aumentou ainda mais com a chegada dos jogos de tabuleiro moderno. E, assim que passei a conhecer vários jogos antigos e recentes que utilizassem tabuleiros modulares, comecei a refletir sobre a base matemática ou, mais especificamente, geométrica, de tudo isso (certamente muitos designers também fizeram isso). Não sou um designer de jogos e muito menos um matemático; o conhecimento que pretendo apresentar aqui é resumido, e baseado em algumas leituras na Wikipedia e outros lugares (na ausência de fontes mais rigorosas). No entanto, acho que vale a pena escrever algo acerca do que aprendi. A ideia aqui é simples: apresentar jogos que ilustrem conceitos de geometria relacionados a tesselações e poliformas, com o objetivo de indicação e até mesmo de dar ideias de design para novos jogos de colocação de peças e de tabuleiro modular.
Tesselações
Definição da Wikipedia: tesselação é o recobrimento de uma superfície bidimensional, tendo, como unidades básicas, polígonos congruentes ou não, sem que existam espaços entre eles e de modo que a superfície total seja igual ao espaço particionado.
A regularidade e os padrões formados pelas tesselações encantam a humanidade desde os primórdios, na confecção de tapetes e recobrimento de pisos, paredes e tetos. Suas características e possibilidades têm sido discutidas desde os gregos, passando pela civilização islâmica e a Idade Média, na tradição da geometria integrante do Quadrivium. E, como veremos, as tesselações são desde sempre usadas para estruturar o espaço de diversos jogos de tabuleiro.

Uma das coisas mais curiosas é que apenas três tipos de tesselação são possíveis usando-se apenas um tipo de polígono regular; motivo que levou alguns a chamá-las de tesselações
platônicas. São elas as tesselações com triângulos, quadrados e hexágonos regulares. Tesselações com quadrados regulares são lugar comum em jogos de tabuleiro, principalmente em abstratos como xadrez, damas, mas também incluindo milhares de outros jogos modernos. Tesselações com hexágonos também são comuns, embora começaram a ser mais usadas em RPGs e Wargames. Já as com triângulos são mais raras - lembro-me de
YINSH, o famoso jogo do projeto GIPF,
Masons, um jogo de construção de cidades, e
Cartography, um jogo de colocação de peças baseado em
Go, - embora, como veremos adiante, a utilização de poliformas produz alguns casos bem interessantes, como no jogo
Cronberg, com um tabuleiro contendo triângulos, porém peças no formato de losangos (ou seja, dois triângulos).
Exemplos de tabuleiros com tesselações regulares envolvendo triângulos, quadrados e hexágonos
Uma segunda classe de tesselações é conhecida como tesselações uniformes, semiregulares ou arquimedianas. Estas podem utilizar diferentes tipos de polígonos regulares (e não apenas um) com a condição de cada aresta ter o mesmo tamanho.
Tabuleiros com tesselações uniformes são raros, mas existem. Geralmente aparecem em jogos abstratos, como
Marque e Kesington. Outro exemplo é Octiles, um jogo de colocação de peças bastante semelhante a Tsuro que utiliza uma tesselação com octógonos e quadrados intercalados.
Dois jogos com tesselações uniformes e bastante unusuais: Octiles e Marque
Penso que a dificuldade de se utilizar tesselações uniformes deve-se ao fato de que elas são muito complexas e regulares ao mesmo tempo - o que não é o caso em territórios no mundo real, por exemplo. Para representar um território em um tabuleiro, ou utilizamos unidades irregulares (como em War), ou dividimos em uma grade de movimento regular, utilizando tesselações regulares (quadrados ou hexágonos). Não obstante, em um jogo de colocação de peças, montar uma tesselação uniforme pode não ser óbvio e complicado demais para os jogadores, a não ser que uma lógica de colocação suficientemente clara possa ser implementada.
De qualquer forma, veremos adiante que, com o conceito de poliforma, muitos jogos de colocação de peças acabam revelando tesselações uniformes, como o próprio Carcassonne. Isso acontece pois embora o arranjo das peças forme uma tesselação regular, os elementos presentes nas próprias peças as dividem em unidades menores, e estas formam outras tesselações. Ou seja: muitas tesselações uniformes podem ser também tesselações regulares com seus polígonos "dissecados".
Vale terminar este trecho apresentando outros tipos de tesselações e que geralmente não aparecem em jogos, e talvez pelo mesmo motivo apresentado anteriormente. São elas as
tesselações irregulares (as arestas não têm o mesmo tamanho), tesselações com apenas um polígono, porém sem peças adjacentes por toda a extensão das arestas (non-edge-to-edge) e tesselações com polígonos não-convexos. Apesar das dificuldades já apontadas antes, acredito que são boas ideias de design.
Notre Dame, por exemplo, é um jogo que encanta por seu tabuleiro escalável.
Alguns tipos bem peculiares de tesselações que ainda (não que eu saiba) foram utilizadas em jogos.
Poliformas
Até então, ao lidarmos com tesselações, incluímos diversos tipos de jogos de tabuleiro, inclusive os de tabuleiro fixo e sem colocação de peças. Veremos agora como a teoria das poliformas nos ajudará a compreender especificamente as mecânicas e o design de jogos de tabuleiro modular e colocação de peças.
Uma poliforma é basicamente uma figura construída pela junção de dois ou mais polígonos idênticos. O caso mais conhecido disso é o dos poliminós, ou seja, poliformas envolvendo quadrados. O dominó é um poliminó com dois quadrados (apenas uma figura possível); da mesma forma, podemos definir um triminó como um poliminó de três quadrados - neste caso, teremos duas figuras possíveis. O tetraminó, por sua vez, apresenta 5 figuras possíveis (eliminando-se as figuras espelhadas), que são as conhecidas peças do Tetris. O raciocínio segue - pentaminós, hexaminós, etc.
Triminós, tetraminós, pentaminós e alguns tipos de polimantes (com triângulos)
Repare que a recente onda dos jogos de colocação de peças no estilo "puzzle" envolvem poliminós -
Patchwork,
Bärenpark e
A Feast for Odin. Outro clássico neste estilo é
Blokus.
Poliformas com triângulos equiláteros são chamadas polimantes (da palavra
diamante), e o único jogo que conheço que utiliza este tipo de poliforma é
Blokus Trigon. Poliformas com hexágonos são chamadas polihexágonos, e podemos encontrá-las em jogos como
Xia,
Barony e
Taluva - embora estes contenham apenas um tipo de figura (sem a sensação de "quebra-cabeça" ao se montar o tabuleiro). Polígonos não regulares também podem ser usados - triângulos pitagóricos e losangos, por exemplo.
Moku é uma proposta interessante de colocação de peças em forma de losango, simulando um cenário 3D isométrico. Por fim, também existem as poliformas em 3 dimensões, entre as quais destacam-se os policubos.
Pueblo, por exemplo, é um interessante jogo envolvendo tetracubos. E, é claro, não poderia faltar
Blokus 3D.
Em sequência, peças de Barony, Moku e Pueblo
Kingdomino é um caso interessante de um problema já conhecido na geometria: a tesselação de dominó. Mas também fico pensando em algum jogo envolvendo algum tipo de diforma (ou seja, poliforma com dois polígonos) com um encaixe ainda mais simples - formando, por exemplo, tesselações regulares ou uniformes. Por exemplo, pode-se pensar em uma diforma com dois triângulos isósceles, com a peça resultante no formato quadrado. Tal caso é um exemplo de tesselação de Truchet, também estudada na geometria. Aliás, estes dois triângulos isósceles também podem formar poliformas, chamadas poliábolos.
Em sequência, uma tesselação irregular com dominós (presente em Kingdomino), uma tesselação de Truchet e exemplos de poliábolos.
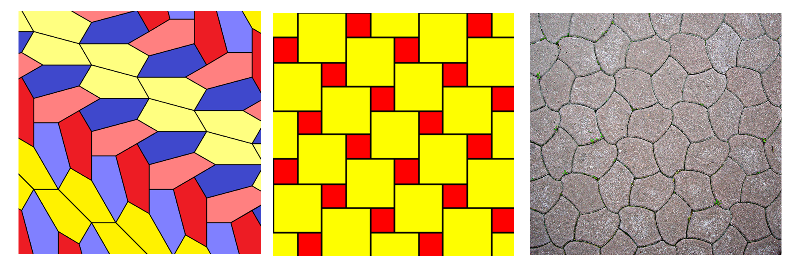
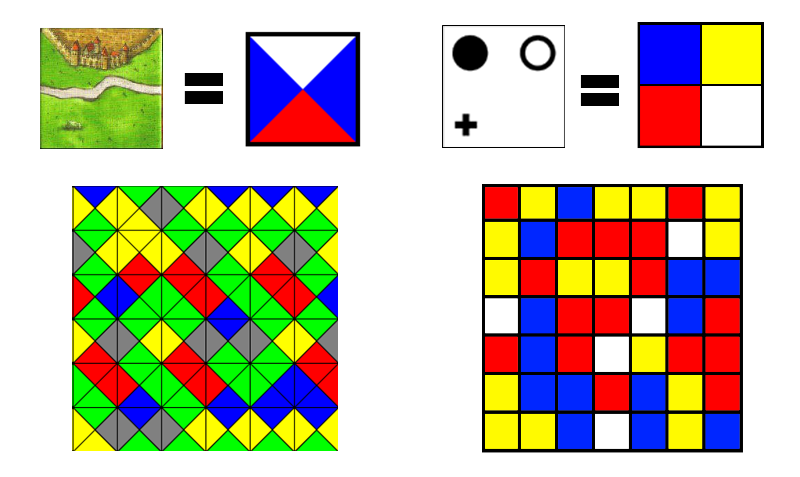
Lembram-se que eu disse que tesselações uniformes podem aparecer nos jogos sob o disfarce das poliformas? Pois bem, vamos lá. Aqui é importante reparar que muitos jogos, principalmente os abstratos, podem ser entendidos como envolvendo uma regra de combinação de certos elementos discretos - números, cores, letras, etc. Explico. O jogo de dominó, por exemplo, contém 6 elementos discretos, ou seja, os seis números que devem ser combinados ao se jogar uma peça. Estes são combinados dois a dois nas peças, e se você já estudou um pouco de análise combinatória, já calculou quantas peças são possíveis. Continuando o raciocínio, um triminó, por exemplo, poderia conter combinações com três números, um em cada quadrado (na verdade, o triminó, como conhecido comercialmente, é um pouco diferente - tem as peças triangulares divididas em três partes). Atribuir elementos discretos a polígonos é conhecido, na geometria, como teoria da coloração de peças (e tesselações). Cada elemento discreto é chamado de cor.
Agora, preste atenção: não seria uma peça de Carcassone um tipo de tetraforma envolvendo três elementos discretos (ou cores) possíveis? A peça é um quadrado, e a tesselação, considerando apenas as peças, é, a princípio, regular. No entanto, cada aresta do quadrado tem um elemento diferente, que deve ser combinado com a aresta da peça adjacente - são eles o campo, a estrada, e a cidade. O resultado é uma tesselação não-regular envolvendo triângulos isósceles (resultantes de um quadrado dissecado) - um caso já conhecido na geometria, chamado de tesselação de Wang.
Um caso diferente pode ser encontrado em outro jogo de peças quadradas:
Micropul. Neste caso, as peças consistem em tetraminós que realmente formam tesselações regulares, com quadrados, quando observadas a nível de elementos discretos - isto porque os elementos discretos estão dispostos nos vértices, e não nas arestas.
Gardens é um jogo que envolve tanto arestas como vértices - são oito elementos em cada peça, no total. No caso de peças hexagonais, o mesmo raciocínio pode ser aplicado aos jogos
Tantrix e
Palago - o primeiro divide as peças pelas arestas, e o segundo, pelos vértices.
Entendendo as peças de Carcassonne e Micropul como poliformas
A ideia de dissecar polígonos - ou mesmo poliformas - para construir diferentes tesselações pode inclusive ser interessante para tabuleiros modulares com espaços de tamanhos variáveis. Pense em peças como do tabuleiro de Xia com divisões irregulares de espaços, variando de peça para peça? Conheço apenas um jogo que faz isso:
Cartography, com peças triangulares, e divisões internas irregulares. Estou esperando mais...
Mas voltando à ideia de cores ou elementos discretos, talvez já esteja óbvio, mas jogos como Patchwork envolvem poliminós com apenas um tipo de elemento em cada quadrado - a regra é apenas preencher o tabuleiro. A coisa pode ficar mais complicada caso algumas regras de colocação sejam adicionadas, como o clássico
Cilada.
Um outro tipo de poliforma que vale citar é o da poliaresta (ou, em inglês,
polistick): formas que consistem em diferentes arestas em torno de polígonos regulares. Por exemplo: são possíveis duas biarestas quadradas e três biarestas triangulares (conecte duas arestas em uma tesselação regular e observe quantas são possíveis).
Desconheço, mas acharia muito interessante encontrar, algum jogo que utilize biarestas, triarestas e assim por diante. (Se algum designer gostou, meu conselho é fazer isso logo, antes que o Uwe Rosenberg, em sua recente onda de jogos com poliminós, chegue primeiro). Quoridor (também conhecido como Bloqueio) apresenta biarestas em um tabuleiro quadrado, mas apenas de um tipo (reta).
Masons e o próprio
Catan, por sua vez, apresentam monoarestas.
Jogos envolvendo poliarestas. Em sequência: Quoridor, Masons e Catan
Uma proposta de classificação
Falamos de muitos jogos e muitas ideias diferentes de se desenvolver um tabuleiro modular ou jogo de colocação de peças. Talvez uma forma de visualizar melhor os jogos, e até mesmo observar algumas lacunas - ou seja, jogos que ainda não foram desenvolvidos, mas que seriam bem interessantes - seja propor um tipo de ficha de classificação dos jogos de tabuleiro modular. Observe:
Carcassonne
Polígono(s) básico(s): triângulo isósceles
Peça: tetraforma (formato de quadrado)
Número de elementos: 3
Barony
Polígono(s) básico(s): hexágono
Peça: tetrahexágono
Número de elementos: 5
Patchwork
Polígono(s) básico(s): quadrado
Peça: poliminós diversos
Número de elementos: 1
Polígono(s) básico(s): quadrado
Peça: monominó
Número de elementos: infinito...
Cartography
Polígono(s) básico(s): vários (dependendo da peça)
Peça: diforma ou triforma (formato triangular)
Número de elementos: 1? (complicado, uma vez que o que diferencia as peças não são os espaços ou cores, mas as separações entre os mesmos - poliarestas?)
Como pode-se observar, a classificação não é completa e nem pretende mesmo ser exaustiva.
Enfim, espero que o presente artigo tenha sido útil ao apresentá-lo a novos jogos e colocar algumas ideias na sua cabeça. Pergunto: e você, conhece algum jogo que não foi citado aqui que utiliza alguma geometria interessante de colocação de peças? Comente!